Nesting algorithm: how it works in Manufacturing Toolkit

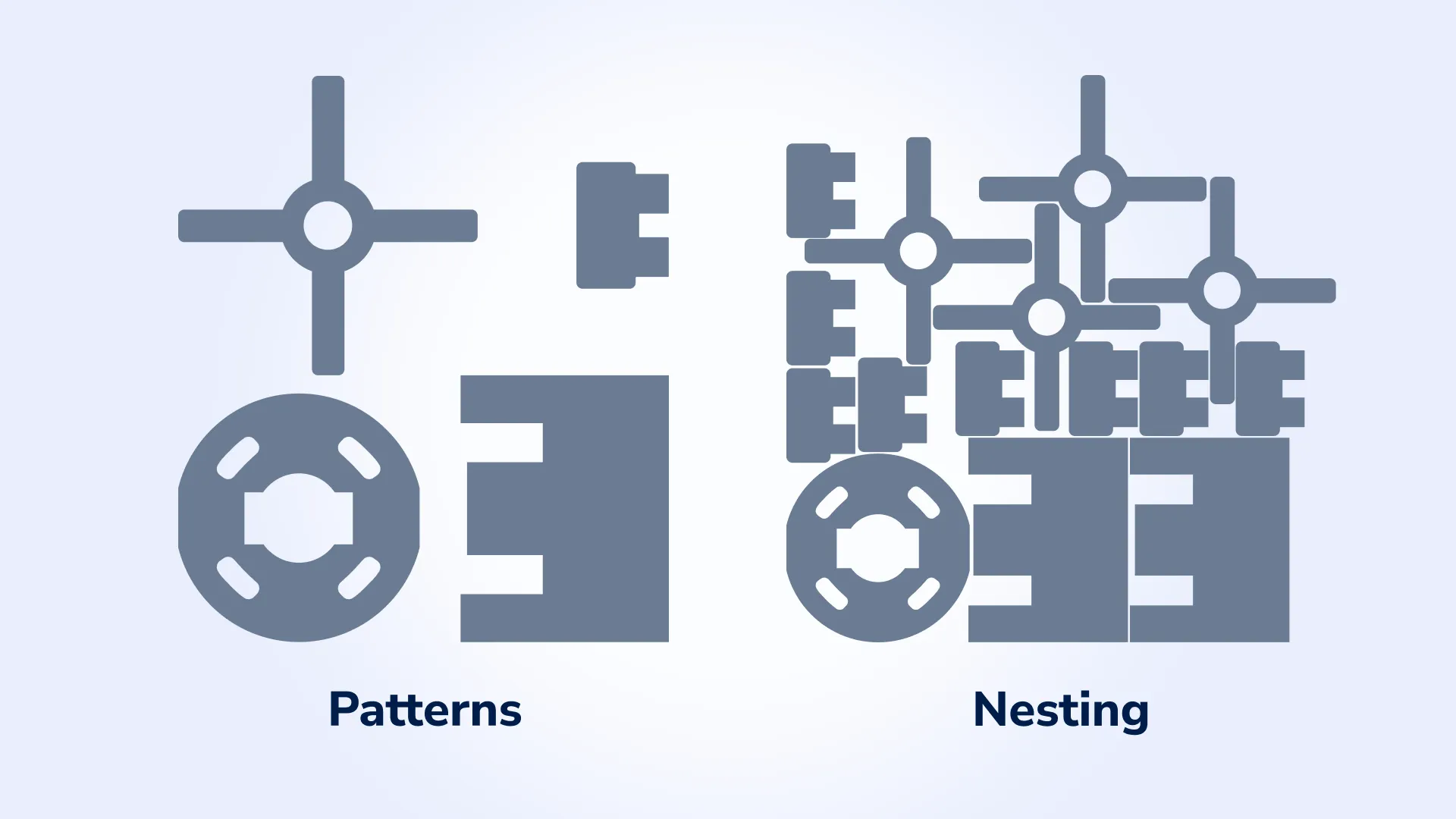
In the world of manufacturing, every square millimeter of material counts. Wasted material not only affects the bottom line but also contributes to environmental challenges. Recognizing this, our team introduced a robust Nesting algorithm in CADEXSOFT Manufacturing Toolkit—a solution designed to optimize how patterns are arranged on raw material sheets. In this blog post, we’ll explore the problem manufacturers faced, the effective solution we implemented, and what we achieved.

Problem: inefficient material usage 

Manufacturing processes often require cutting patterns from large sheets of raw materials like metal, plastic, or wood. The challenge lies in arranging these patterns—or “nesting” them—in a way that minimizes waste.

Manual arrangement is too time-consuming and resource-intensive, while straightforward methods might solve small-scale problems but fail to handle real-world nesting challenges effectively. For example:

• Simple geometric approaches: They rely on basic placement patterns like stacking patterns  in rows or columns, often using bounding boxes, which are less space-efficient than exact contours.
• Greedy algorithms: They focus on immediate fit but don’t optimize the overall layout, leading to inefficiencies.

Additionally, straightforward methods often come with inherent limitations:

• Fixed-orientation placements: Patterns are limited to specific rotations or positions, reducing flexibility and material utilization.
• Limited handling of complex shapes: Struggling with irregular or intricate geometries, which are common in manufacturing.

These approaches and limitations lead to higher material costs, longer production times, and increased waste—a significant problem for manufacturers.

Our solution: two-tiered nesting algorithm   

Since there’s no exact solution for this problem in general, we turned to widely used heuristic methods. Our solution involves a two-step nesting algorithm that applies common computational techniques:

1. Genetic Algorithm (GA): finding the best configurations

The GA serves as the first layer in our process, providing a well-established approach for solving complex optimization problems like nesting. It helps determine the optimal sequence and orientation of patterns. Here’s how it works:

• Initialization: The process begins by defining the raw material sheet sizes and the patterns to be nested.
• Creation of initial generation: The algorithm generates a random initial population of arrangements, with each arrangement represented by a vector. This vector defines the order in which patterns are considered for placement, along with their potential orientations. For example, an arrangement vector might look like 12345, where each number corresponds to a specific pattern’s identifier.
• Evaluation: Each arrangement is scored based on its Placement Efficiency—a metric representing the ratio of the total area of the patterns to the bounding box area of their arrangement on a sheet. This measures how effectively the available space is utilized. Mathematically, the Placement Efficiency (E) can be expressed as:

• Evolution: To improve arrangements across generations, the GA employs crossover and mutation operations:

Crossover combines two parent arrangements to produce a new offspring arrangement. As an example, let’s consider two parent vectors: 12345 and 35142.

First, a crossover point is chosen (e.g., after the first three elements of the first parent). The offspring then takes the first three elements from the first parent: 123.

The remaining elements are filled in the order they appear in the second parent, skipping duplicates. Therefore, the resulting offspring vector is 12354. This vector is then passed to the Placement Strategy, where the parts are arranged on the sheet based on the given order and orientations.

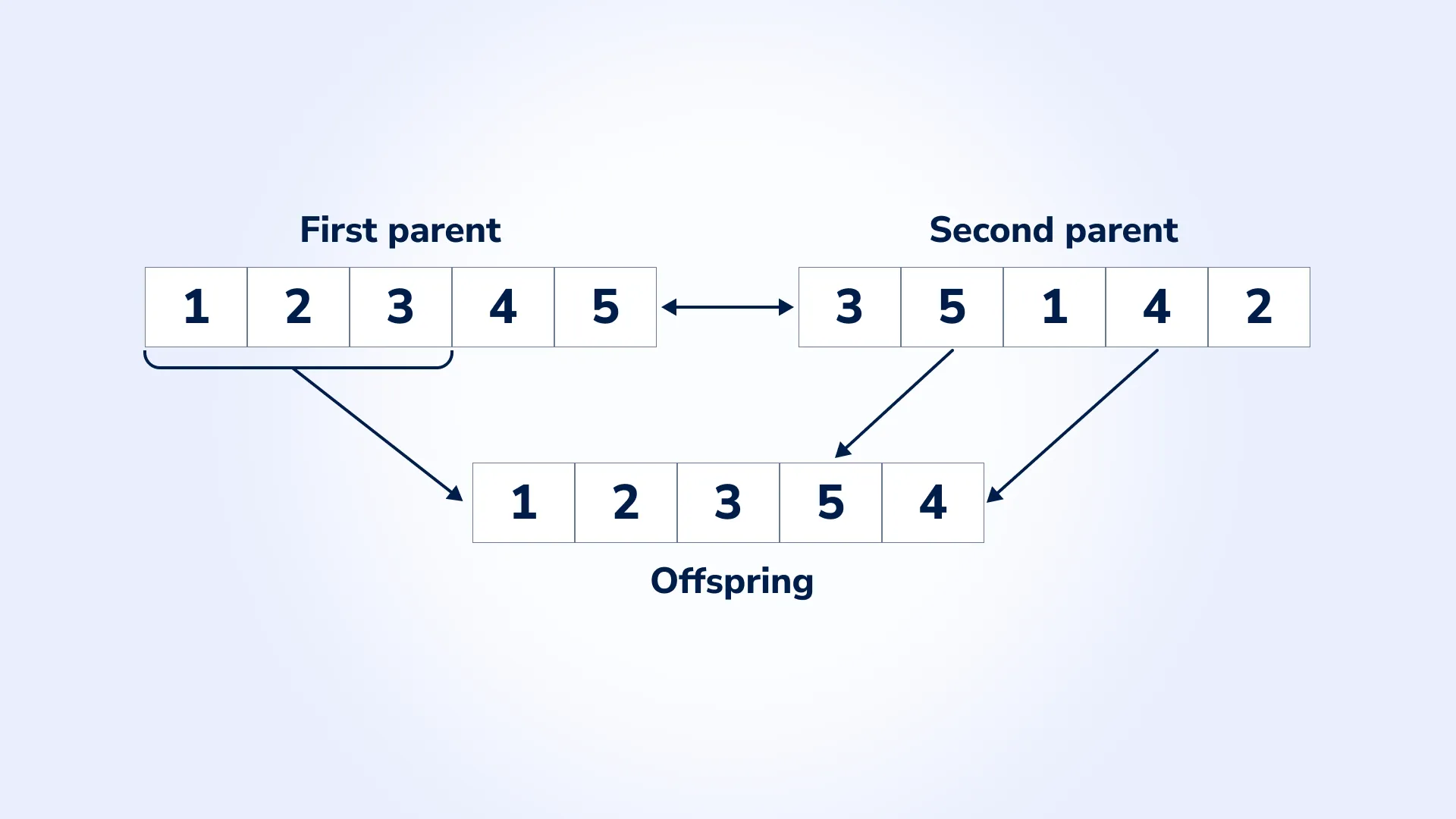
Mutation introduces random changes to an arrangement vector to explore new configurations and avoid local optima. Let’s consider an example: a mutation might swap two elements in the vector 12345, resulting in 13245.

Alternatively, it could randomly shuffle a subset of the vector to create a new variation. These small alterations ensure diversity in the population and help the algorithm discover better solutions.

• Selection: The best arrangements from the new and previous generations are selected and carried forward to the next iteration, where the process repeats to refine and improve the overall arrangement.
• Final selection: After several iterations, the most efficient arrangement is chosen as the final solution.

2. Placement Strategy: ensuring precision  

During the GA process, the Placement Strategy algorithm is used to take into account placement constraints while creating new populations. This algorithm calculates geometric arrangements to ensure that patterns  fit together without overlapping and remain within the sheet boundaries. It also adheres to conditions such as the minimum distances between the patterns  and the edges of the sheet. 

The Placement Strategy works by attempting to arrange the patterns according to the sequence defined by the arrangement vector. The algorithm follows a left-bottom strategy, where each pattern is positioned as close as possible to the left-bottom corner of the sheet while ensuring no overlaps or violations of boundary conditions occur.

To enhance efficiency, the Placement Strategy calculations were parallelized, allowing the algorithm to handle complex shapes and large datasets faster.

Nesting parameters 

Our nesting algorithm supports a comprehensive set of parameters that you can customize to fit your specific requirements.

1. Iteration count: Defines the number of iterations the Nesting Algorithm will perform.
2. Generation size: Specifies the number of arrangements in each generation for the Genetic Algorithm.
3. Mutation rate: Controls the probability of random mutations occurring during the GA optimization process.
4. Curve tolerance: Defines the side length of squares used for polygonal approximation of curves.  Larger values lead to coarser approximations and faster computation, while smaller values improve accuracy at the cost of increased processing time.
5. Part-to-part distance: Sets the minimum allowable distance between patterns to avoid overlaps.
6. Part-to-sheet boundary distance: Ensures a specified margin between patterns and the sheet boundary.
7. Mirror control: Allows the inclusion or exclusion of mirrored patterns during nesting.
8. Rotation count: Limits the number of rotations considered for each pattern during placement.

References and sources 

Our team leveraged research from widely recognized sources, along with our own experience in manufacturing, to guide our use of  the Genetic Algorithm (GA) and the Placement Strategy in nesting optimization. Our approach drew inspiration from a variety of sources, including the following studies:

Source 1. Genetic algorithm based nesting method with considering schedule for sheet metal processing
Source 2. No fit polygon for nesting problem solving with hybridizing ant algorithms
Source 3. Fast neighborhood search for the nesting problem 
Source 4. Genetic algorithm based 2d nesting of sheet metal parts

Challenges and solutions  

The development of an effective nesting algorithm is a complex task that involves overcoming several technical obstacles. From handling intricate geometries to optimizing computational efficiency, each challenge required innovative solutions to ensure robust and precise placement of patterns. Below, we discuss two key challenges encountered during development and the strategies implemented to address them.

Handling complex shapes

Accurately processing irregular patterns presented a challenge, especially when dealing with intricate patterns geometries.

Solution

We implemented an approximation technique that converts complex shapes into polygons by dividing the shape’s bounding box into smaller squares. These squares were then used to construct a polygon that closely resembles the original shape. By adjusting the square size, we achieved precise approximations, enabling effective nesting for various sheet sizes and pattern forms.

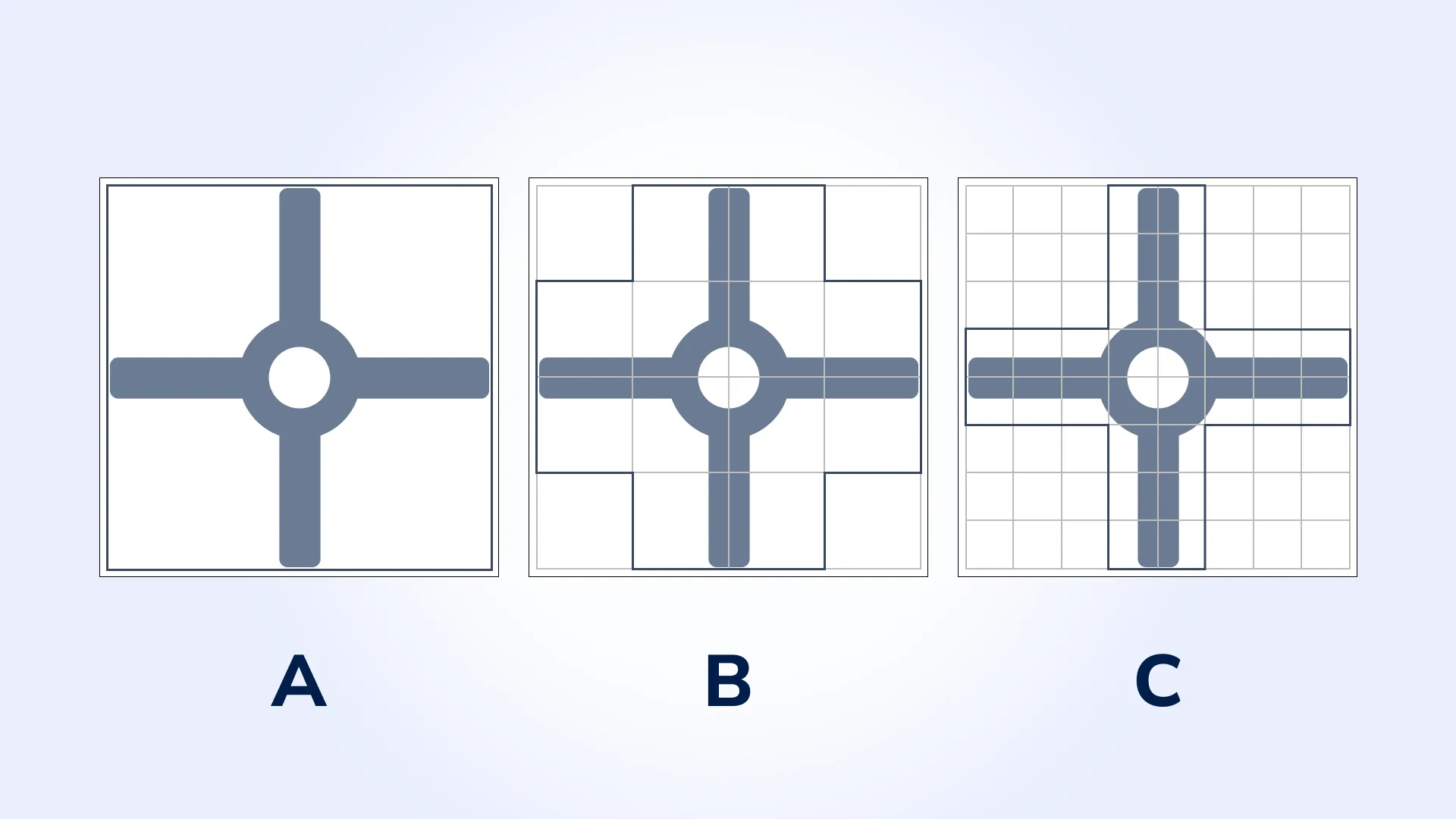
Intersection detection

Initially, detecting intersections required computationally intensive polygon overlap checks. This approach was inefficient, particularly when dealing with intricate shapes or large datasets, as it consumed substantial resources and slowed down processing.

Solution

Our team optimized the algorithm to use analytical curves for detecting overlaps instead of traditional polygon checks. This enhancement significantly reduced computational overhead and improved the speed and precision of placement evaluations.

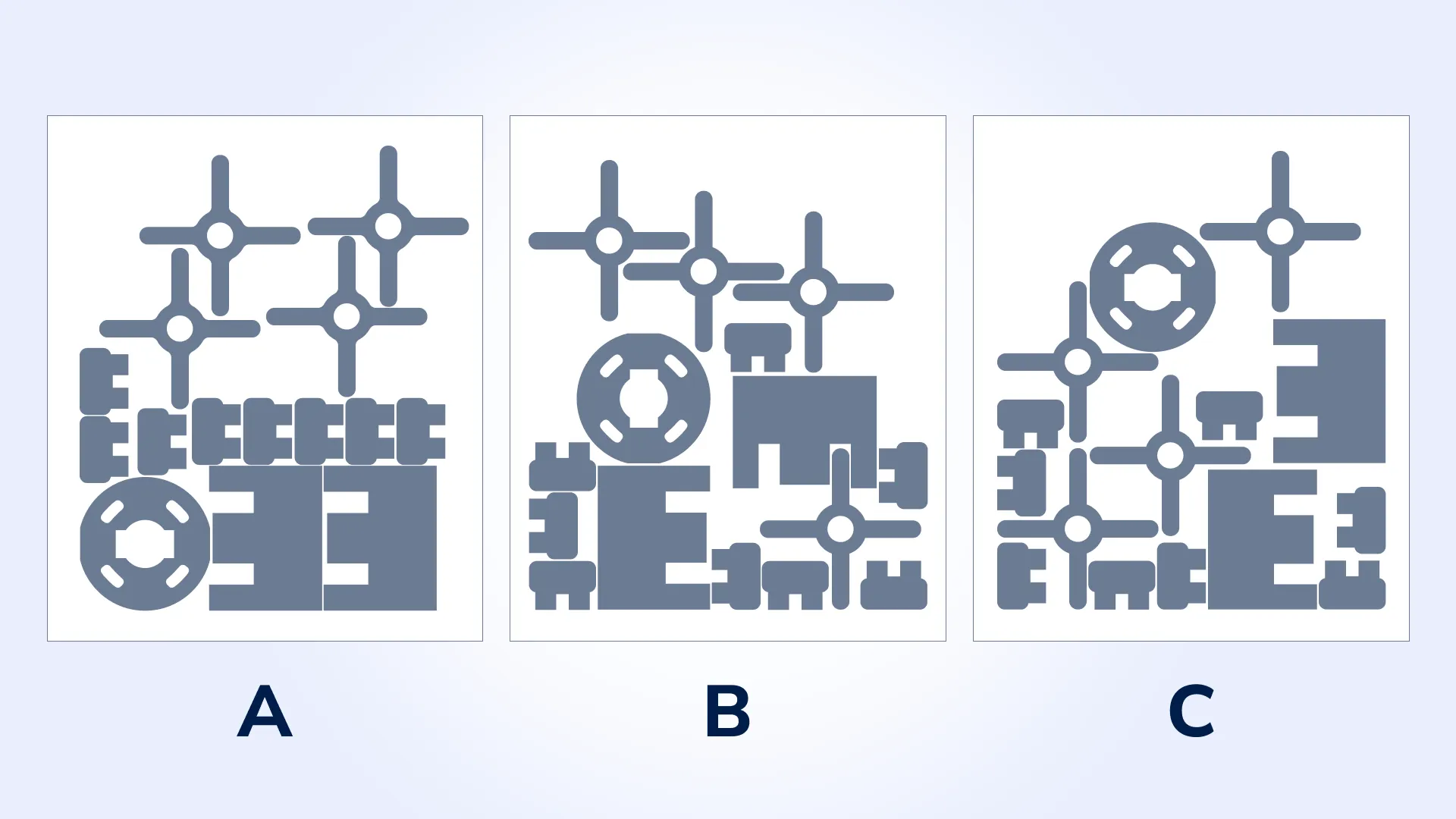
The resulting nesting algorithm step-by-step 

To showcase the capabilities of our nesting algorithm, we’ll walk through a practical example, demonstrating how it efficiently arranges patterns on a sheet. This example highlights the entire process—from input to optimization—offering a clear picture of the algorithm’s functionality and benefits.

 Step 1: input data 

The algorithm begins with input data:

1. Sheet dimensions: A rectangular sheet measuring 300mm x 350mm.
2. Unique shapes: Four irregularly shaped patterns with specified dimensions and orientations.
3. Quantities: Each unique pattern repeats a specific number of times.

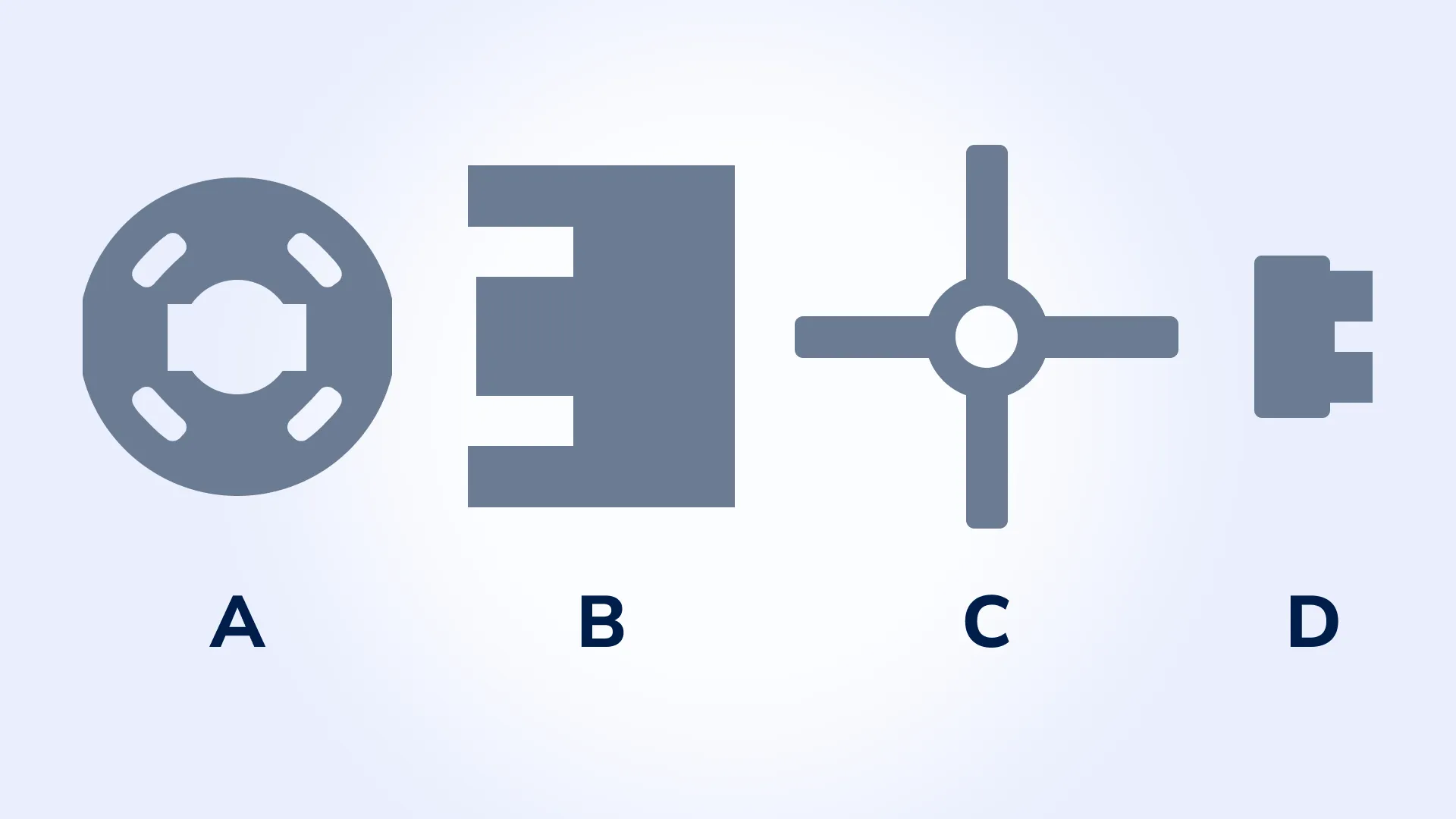
The nesting algorithm operates based on the following parameter settings:

1. Iteration count (10): The algorithm performs 10 iterations, refining the arrangements in each cycle to improve efficiency.
2. Generation size (10): Each generation contains 10 arrangements (individuals), ensuring diversity and a sufficient search space for optimization.
3. Mutation rate (0.1): A 10% mutation rate introduces random variations in the arrangements to explore new possibilities and prevent local optima.
4. Curve tolerance (1): The complexity of shapes is approximated with polygons using a grid size of 1 unit, balancing precision and computational efficiency.
5. Part-to-part distance (0.1): A minimum distance of 0.1 is enforced between patterns, ensuring they are not placed closer than this threshold.
6. Part-to-sheet boundary distance (0.0): Patterns are allowed to be placed right up to the sheet edges without any margin.
7. Mirror control (false): Mirroring of patterns is disabled because orientation variations are already accounted for by the Rotation count (4).
8. Rotation count (4): Each pattern can be rotated into one of four predefined orientations (e.g., 0°, 90°, 180°, 270°).

Step 2: initial placement 

In the initial step, patterns are placed on the sheet randomly using a Placement Strategy to avoid overlaps and ensure boundary constraints are met. This process is repeated for a number of layouts equal to the Generation Size, which specifies the total number of arrangements in each generation. These initial layouts are not optimized, serving as a baseline for the subsequent evolutionary process.

Step 3: optimization process 

The algorithm applies its optimization techniques to improve the arrangement:

1. Placement Strategy: Determines valid positions for patterns, ensuring no overlaps and adherence to constraints.
2. Crossover and Mutation: These genetic operations iteratively refine the layout to achieve higher Placement Efficiency.

After optimization, the algorithm produces a layout that:

1. Places all patterns within the sheet boundaries without overlaps.
2. Satisfies all constraints, such as minimum distances between patterns and edges.
3. Maximizes material utilization.

This step-by-step example offers a clear and compelling visualization of how our algorithm transforms a complex nesting challenge into an optimized and efficient solution.

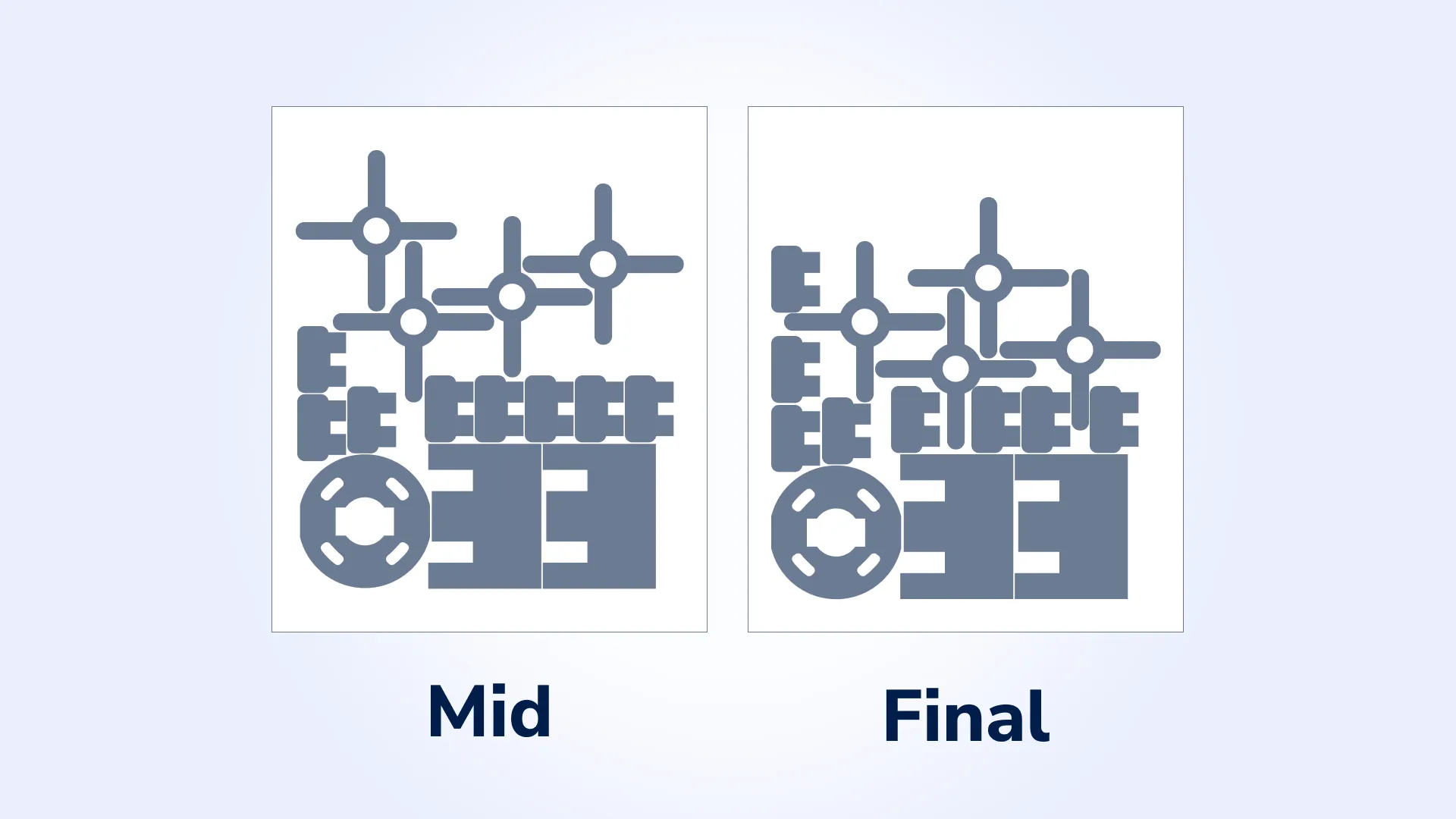
Results achieved

Implementing this Nesting solution yielded immediate benefits:

1. Versatility: The solution easily adapts to different patterns shapes, sizes, materials, and sheet dimensions, making it suitable for both small and large-scale production needs.
2. Material savings: Manufacturers observed a significant reduction in material waste compared to traditional methods, allowing for more efficient use of raw materials.
3. Time efficiency: The automated process made nesting faster, saving valuable time and allowing resources to be allocated more effectively.

The Nesting feature in Manufacturing Toolkit showcases how advanced algorithms can tackle real-world challenges in manufacturing. By combining Genetic Algorithms with Placement Strategy, our team’ve created a solution that drives efficiency, reduces waste, and supports sustainable practices.

The journey doesn’t end here—optimization is a continuous process. We’re committed to evolving our tools to meet the ever-changing needs of modern manufacturers. If you are interested in this solution, contact us to explore how our advanced algorithms can optimize your production line. Our team is ready to provide insights and help you achieve greater efficiency and profitability.

Get your trial of Manufacturing Toolkit here.